Định nghĩa

Độ lệch chuẩn (tiếng Anh: Standard Deviation) là một công cụ thống kê đo lường độ phân tán của tập dữ liệu so với giá trị trung bình của nó và được tính là căn bậc hai của phương sai.

Độ lệch chuẩn (Standard Deviation)

Khái niệm

Độ lệch chuẩn trong tiếng Anh là Standard Deviation.

Độ lệch chuẩn là một phép đo lường trong thống kê và trong tài chính được áp dụng cho tỉ lệ hoàn vốn hàng năm của một khoản đầu tư, để làm sáng tỏ những sự biến động trong lịch sử khoản đầu tư đó. 

Độ lệch chuẩn của một cổ phiếu càng lớn, hay phương sai giữa giá cổ phiếu và giá trị trung bình càng lớn, cho thấy phạm vi giá giao động càng rộng. Ví dụ, một cổ phiếu bất ổn có độ lệch chuẩn cao, trong khi độ lệch chuẩn của một cổ phiếu blue-chip ổn định thường khá thấp.

Độ lệch chuẩn được tính là căn bậc hai của phương sai, được tính bằng cách xác định sự chênh lệch giữa mỗi điểm dữ liệu so với giá trị trung bình. Nếu một điểm dữ liệu nằm xa giá trị trung bình, điểm đó có độ lệch cao trong tập dữ liệu, dữ liệu càng có độ dàn trải rộng thì độ lệch chuẩn càng cao.

Công thức tính độ lệch chuẩn

Trong đó:

x_i là giá trị của điểm i trong tập dữ liệu

x̄ là giá trị của tập dữ liệu

n là tổng số quan sát trong tập dữ liệu

Giá trị x trung bình được tính bằng cách tổng tất cả các quan sát và chia cho số quan sát.

Phương sai cho mỗi điểm dữ liệu được tính bằng cách trừ giá trị của quan sát với giá trị trung bình. Kết quả sau đó được bình phương và được chia cho số quan sát trừ một.

Căn bậc hai của phương sai để tìm độ lệch chuẩn.

Sử dụng độ lệch chuẩn (Standard Deviation)

Độ lệch chuẩn là một công cụ đặc biệt hữu ích trong xây dựng chiến lược đầu tư hay trong giao dịch vì nó đo lường mức độ biến động của thị trường và chứng khoán, cuối cùng dự đoán hiệu quả đàu tư. 

Ví dụ, nhà đầu tư cần cân nhắc rằng các quỹ tăng trưởng tích cực thường có độ lệch chuẩn cao hơn so với các chỉ số chứng khoán, vì các nhà quản lý danh mục đầu tư của họ đặt cược mức rủi ro lớn hơn để đạt được lợi nhuận cao hơn mức trung bình.

Độ lệch chuẩn thấp hơn không nhất thiết là tốt hơn mà tất cả phụ thuộc vào khoản đầu tư mà nhà đầu tư đang có và việc họ có sẵn sàng chấp nhận rủi ro hay không. Khi có sự biến động trong danh mục đầu tư, các nhà đầu tư nên xem xét khả năng chịu đựng của cá nhân họ đối với sự biến động này và mục tiêu đầu tư tổng thể của họ. 

Các nhà đầu tư ưa thích rủi ro có thể thoải mái với những chiến lược đầu tư vào các tài sản có độ biến động cao hơn mức trung bình, trong khi các nhà đầu tư bảo thủ (hay e ngại rủi ro) thì không.

Độ lệch chuẩn là một trong những biện pháp đo lường rủi ro cơ bản chính mà các nhà phân tích, quản lý danh mục đầu tư, cố vấn tài chính sử dụng. Một độ chênh lệch lớn cho thấy mức lợi nhuận của một quỹ đang chênh lệch nhiều so với mức lợi nhuận dự kiến. Do tính chất dễ hiểu, công cụ thống kê này thường xuyên được sử dụng để báo cáo cho các khách hàng và nhà đầu tư.

Độ lệch chuẩn so với phương sai

Phương sai được tính bằng cách lấy giá trị trung bình của các quan sát trừ đi giá trị trung bình, sau đó bình phương từng kết quả này và cuối cùng lấy giá trị trung bình của các kết quả này. Độ lệch chuẩn là căn bậc hai của phương sai.

Phương sai giúp xác định độ dàn trải của quan sát khi so sánh với giá trị trung bình. Phương sai lớn cho thấy có nhiều sự biến động trong các giá trị của tập dữ liệu và có thể có khoảng cách lớn hơn giữa giá trị các quan sát với nhau. Nếu tất cả các quan sát đứng gần nhau, phương sai sẽ nhỏ hơn. Tuy nhiên, khái niệm này khó hiểu hơn nhiều so với độ lệch chuẩn, do phương sai biểu thị một kết quả bình phương.

Độ lệch chuẩn thường dễ hình dung và dễ áp dụng hơn. Độ lệch chuẩn được biểu thị trong cùng một đơn vị đo lường với dữ liệu, sử dụng độ lệch chuẩn, các nhà thống kê có thể xác định liệu dữ liệu có phân phối chuẩn hay có mối quan hệ toán học khác. 

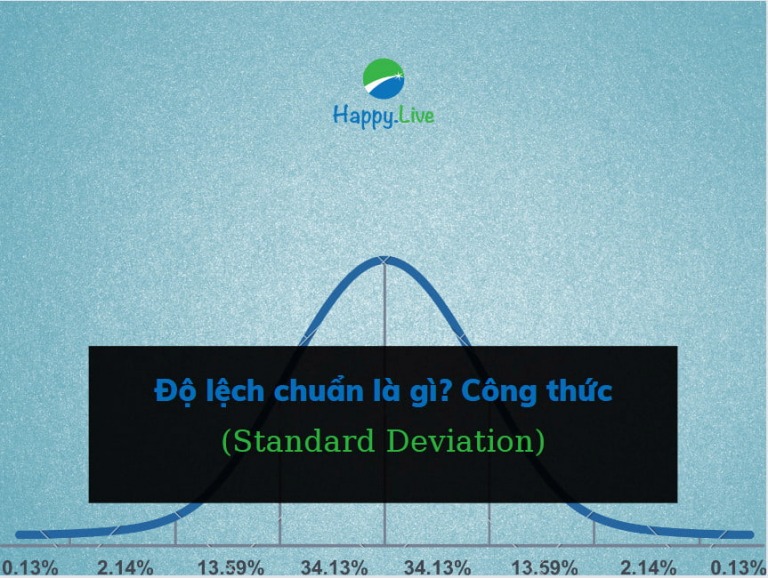
Nếu dữ liệu có một phân phối chuẩn, thì 68% quan sát sẽ nằm trong một biên độ lệch chuẩn đến điểm trung vị hoặc trung bình. Phương sai do bình phương lên khiến nhiều điểm dữ liệu nằm ngoài độ lệch chuẩn, hay còn gọi là các điểm ngoại lai. Phương sai nhỏ hơn dẫn đến nhiều dữ liệu gần với giá trị trung bình.

Hạn chế lớn nhất của việc sử dụng độ lệch chuẩn là nó có thể bị ảnh hưởng bởi các điểm ngoại lai và các giá trị âm. Độ lệch chuẩn có giả định là phân phối chuẩn và xem tất cả sự không chắc chắn là rủi ro, ngay cả khi nó có lợi cho nhà đầu tư, ví dụ như khi lợi nhuận đạt mức trên trung bình.

Ví dụ về độ lệch chuẩn

Giả sử chúng ta có các quan sát 5, 7, 3 và 7, tổng cộng 22. Sau đó, bạn sẽ chia 22 cho số quan sát, trong trường hợp này là 4 được 5,5. Ta có trung bình là: x̄ = 5,5 và N = 4.

Phương sai được xác định bằng cách trừ mỗi quan sát cho giá trị trung bình, ta được lần lượt các kết quả là -0,5, 1,5, -2,5 và 1,5. Mỗi giá trị này sau đó được bình phương, bằng 0,25, 2,25, 6,25 và 2,25. Công các giá trị bình phương sau đó chia cho giá trị N trừ 1, bằng 3, cho kêt quả phương sai xấp xỉ 3,67.

Căn bậc hai của phương sai có độ lệch chuẩn là khoảng 1.915.

Ví dụ về độ lệch chuẩn trong đầu tư tài chính, xem xét cổ phiếu của Apple (AAPL) trong năm năm qua thấy được lợi nhuận cho AAPL là 37,7% cho năm 2014, -4,6% cho năm 2015, 10% cho năm 2016, 46,1% cho năm 2017 và -6,8% cho năm 2018. Lợi nhuận trung bình trong năm năm là 16,5%.

Lấy lợi nhuận của mỗi năm trừ giá trị trung bình được 21,2%, -21,2%, -6,5%, 29,6% và -23,3%. Tất cả các giá trị này sau đó được bình phương được 449.4, 449.4, 42.3, 876.2 và 542.9. Tính được phương sai là 590.1, sau đó các giá trị bình phương được cộng lại với nhau và chia cho 4 (N – 1). Căn bậc hai của phương sai được lấy để có độ lệch chuẩn là 24,3%. 

Nguồn: dongvon.doanhnhanvn.vn (link)