Định nghĩa

Phân phối xác suất loga chuẩn (tiếng Anh: Log-Normal Distribution) là phân phối thống kê các giá trị logarit từ một phân phối chuẩn có liên quan.

Khái niệm 

Phân phối xác suất loga chuẩn hay phân phối log-normal trong tiếng Anh là Log-Normal Distribution.

Phân phối log-normal có thể được chuyển hóa thành phân phối chuẩn và ngược lại bằng cách sử dụng các tính toán logarit liên quan.

Phân phối chuẩn là phân phối xác suất của các kết quả đối xứng hoặc tạo thành một đường cong hình chuông. Trong một phân phối chuẩn, 68% kết quả nằm trong một độ lệch chuẩn và 95% nằm trong hai độ lệch chuẩn so với giá trị trung bình.

Hầu hết mọi người đều biết đến phân phối chuẩn tuy nhiên phân phối xác suất loga chuẩn có thể là một khái niệm khá mới mẻ. Một phân phối chuẩn có thể được chuyển đổi thành phân phối log-normal bằng các hàm toán học logarit. Các phân phối log-normal chỉ có thể sử dụng khi tập hợp các biến ngẫu nhiên có phân phối chuẩn.

Một vài lí do để sử dụng phân phối log-normal song song với phân phối chuẩn là hầu hết các phân phối log-normal là kết quả của việc lấy cơ số tự nhiên e = 2.718. Tuy nhiên, phân phối log-normal có thể thay đổi phạm vi bằng cách sử dụng một cơ sở khác có ảnh hưởng đến hình dạng của phân phối log-normal.

Nhìn chung, phân phối log-normal biểu diễn logarit của các biến ngẫu nhiên từ một phân phối chuẩn. Logarit được gọi là số mũ mà cơ số phải được mũ lên để tạo ra một biến ngẫu nhiên (x) có thể tìm thấy dọc theo đường cong của phân phối chuẩn.

Ứng dụng của Phân phối log-normal trong tài chính

Phân phối chuẩn có một vài vấn đề mà phân phối log-normal có thể giải quyết. Phân phối chuẩn cho phép các biến ngẫu nhiên có thể âm trong khi phân phối log-normal có tất cả các biến đều dương.

Một trong những ứng dụng phổ biến nhất của phân phối log-normal được sử dụng trong tài chính là trong quá trình phân tích giá cổ phiếu. Lợi nhuận tiềm năng của một cổ phiếu có thể có phân phối chuẩn. Giá của cổ phiếu tuy nhiên có thể được vẽ thành biểu đồ của phân phối log-normal. Đường cong phân phối log-normal có thể được sử dụng để giúp xác định tốt hơn lợi nhuận gộp dự kiến mà cổ phiếu có thể đạt được trong một khoảng thời gian nhất định.

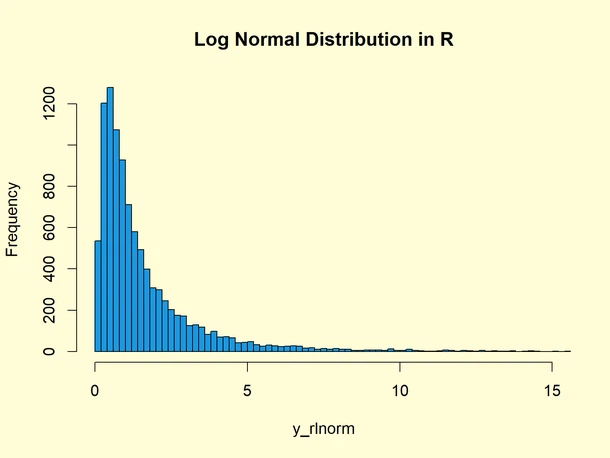
Lưu ý rằng phân phối log-normal thường bị lệch với đuôi phải dài do giá trị trung bình thấp và phương sai cao trong các biến ngẫu nhiên.

Theo Instopedia

Các bạn có thể tham khảo thêm về các thuật ngữ khác tại đây