Các tỷ lệ Fibonacci được sử dụng trong thị trường tài chính không chỉ là tỷ lệ vàng 1.618 mà còn các biến thể của nó. Các biến thể này được tính theo mối quan hệ căn bậc hai. 

Bạn có biết:

• Thị trường tài chính tuân theo các luật của tự nhiên là Sóng Elliott và Tỷ lệ Fibonacci.
• Tỷ Lệ Fibonacci là nền tảng của Sóng Elliott theo khẳng định của cha đẻ lý thuyết này, ông R.N.Elliott.
• Fibonacci Cluster và FIbonacci Divider là những công cụ giúp các nhà giao dịch sóng Elliott tìm ra các mục tiêu giá có độ tin cậy cao.

Sóng Elliott và tỷ lệ Fibonacci

Năm 1938, khi phát hiện ra quy luật sóng Elliott, Ông R.N.Elliott gọi mẫu hình chuyển động giá là “Sóng”. Tuy nhiên, tên gọi chính thức mà Elliott muốn nhấn mạnh lúc đó “Luật Tự Nhiên” trong cuốn sách “Nature’s law: The secret of the universe (Elliott Wave). Nói cách khác, Elliott muốn nói rằng, sóng Elliott chính là quy luật của tự nhiên. Elliott tin rằng, thị trường tài chính cũng phải tuân theo quy luật tự nhiên này.

Trong cuốn sách, Elliott khẳng định, “FIbonacci chính là nền tảng chính của sóng”. Tên gọi “sóng Elliott” mà chúng ta biết đến ngày nay là do Robert Prechter đặt ra trong cuốn sách nổi tiếng “Nguyên Lý Sóng Elliott (Elliott Wave Principle)” (1978). Trải qua hơn 30 năm, cuốn sách Nguyên Lý Sóng trở nên phổ biến và Robert Prechter đã có công phổ biến Lý Thuyết Sóng (được gọi là Sóng Elliott) đến cộng đồng phố Wall, điều mà cha đẻ của lý thuyết này không làm được.

Thực vậy, khi phân tích sóng Elliott, một nhà giao dịch phải phân tích ba khía cạnh:
– Cấu trúc sóng: Nghĩa là hình dạng và cấu trúc trúc bên trong của sóng đẩy và sóng hiệu chỉnh.
– Tỷ lệ Fibonacci giữa các sóng – về khía cạnh giá.
– Tỷ lệ Fibonacci giữa các sóng – về khía cạnh thời gian.

Giá và thời gian của các sóng thường có mối quan hệ với nhau theo tỷ lệ Fibonacci. Trong phân tích sóng, tỷ lệ Fibonacci quan trọng nhất là 0.618 hay 61.8%, được gọi là Tỷ Lệ Vàng hay Sự Cân Bằng. Nó được ký hiệu bằng chữ cái Hy Lạp là Phi (ϕ). Nghịch đảo của tỷ lệ vàng là 1.618. Phi là một con số mà khi cộng với 1, cũng bằng nghịch đảo của nó. Nếu chúng ta lấy bình phương của phi hoặc lấy 1 trừ cho phi, kết quả đều bằng 0.382, cũng là một tỷ lệ Fibonacci khác.

Fibonacci tồn tại trong tự nhiên, nghệ thuật, và cả thị trường chứng khoán. Xem các hình sau để thấy vẻ đẹp của Fibonacci:

Các tỷ lệ Fibonacci được sử dụng trong thị trường tài chính

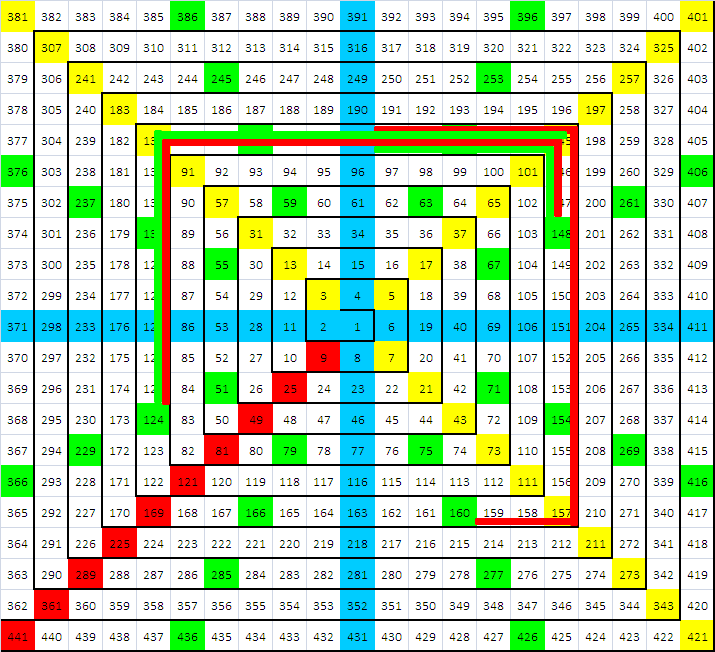
Các tỷ lệ Fibonacci được sử dụng trong thị trường tài chính không chỉ là tỷ lệ vàng 1.618 mà còn các biến thể của nó. Các biến thể này được tính theo mối quan hệ căn bậc hai. Điều này được tiết lộ bởi Gann, khi quan sát mối quan hệ giữa các dãy số từ Kim Tự Tháp. Nó được biết đến với tên gọi Gann Square of Nine. Theo đó, một dãy số khi hoàn tất một vòng quay sẽ được chuyển sang vòng quay tiếp theo bằng mối quan hệ căn bậc hai. Ví dụ, hãy quan sát các con số màu vàng theo hình chéo trong hình Gann Square of Nine. Lấy căn bậc 2 của 65 (khoảng 8.0622…) sau đó cộng cho 2 (kết quả là 10.0622…). Tiếp tục bình phương trở lại ta có kết quả là 101.2490… Xấp xỉ con số tiếp theo là 101.

Mối quan hệ giữa các con số trong Gann Square of Nine chính là quan hệ Căn Bậc Hai

Dựa trên mối quan hệ căn bậc hai, chúng ta có thể tạo ra nhiều biến thể Fibonacci. Các tỷ lệ Fibonacci như sau: 23.6%, 38.2%, 50%, 61.8%,78.6%, 88.6% và 100%; 127%, 161.8%; 200%; 261.8%; 300%; 423%.

Trong đó, mối quan hệ căn bậc hai là:

Căn bậc hai của 0.786 chính là 0.886

Căn bậc hai của 0.618 chính là 0.786

Căn bậc hai của 0.382 chính là 0.618

Riêng Fibo 23.6% được hình thành từ việc lấy 38.2% x 61.8%

Lưu ý, chúng ta để ý 38.2% + 61.8%=1. Thì cặp thứ hai nên là 23.6% + 76.4%=1. Như vậy, chúng ta còn một tỷ lệ khác là 76.4%

Căn bậc hai của 1.618 chính là 1.27

Căn bậc hai của 2.618 chính là 1.618

Mối quan hệ nghịch đảo giữa giữa các Fibonacci:

Nghịch đảo của 0.382 chính là 2.618

Nghịch đảo của 0.618 chính là 1.618

Nghịch đảo của 0.236 chính là 4.23

Nghịch đảo của 0.5 chính là 2

Nghịch đảo của 0.786 chính là 1.27

Sử dụng Vùng Tập Fibonacci (Fibonacci Cluster) để tìm ra các mục tiêu giá có độ chính xác cao.

Lợi thế của sóng Elliott là cung cấp các mục tiêu giá rõ ràng, có độ tin cậy cao. Vì các sóng Elliott có mối quan hệ với nhau theo tỷ lệ Fibonacci nên chúng ta có thể tìm ra vùng tập hợp FIbonacci (Fibonacci Cluster) cho các mục tiêu giá.

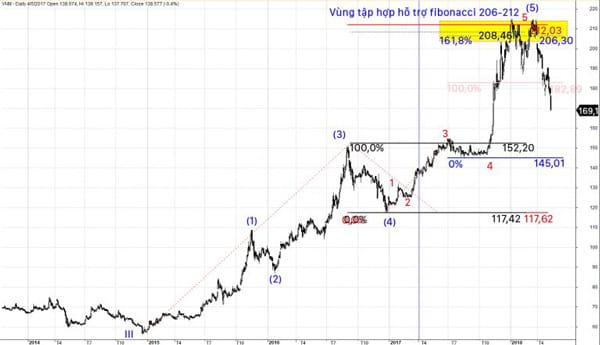
Ví dụ, trường hợp của VNM vào quý 1.2018. Vùng Fibonacci Cluster được xác định là 206-212 được tạo bởi:

Sóng (5)= 1 lần sóng (1)-(3) (từ điểm bắt đầu sóng (1) đến điểm kết thúc sóng (3)).

Sóng (5)= 2.618 lần sóng (4).

Sóng 5 cũng là điểm kết thúc sóng (5)= 1.618 lần sóng 1-3 (từ điểm bắt đầu sóng 1 đến điểm kết thúc sóng 3).

Sử dụng Bộ Chia FIbonacci (Fibonacci Divider) để xác nhận độ tin cậy.

Trong cuốn sách “HƯỚNG DẪN GIAO DỊCH SÓNG ELLIOTT”, Wane Gorman và Jefferey Kennedy đã giới thiệu một công cụ được gọi là “BỘ CHIA FIBONACCI” như một công cụ để kiểm tra độ tin cậy của mục tiêu giá sau khi đã tìm ra Vùng Tập Hợp. Chi tiết cách thức sử dụng bộ chia được trình bày trong cuốn sách.

Đồ thị dưới đây cho thấy, tại điểm 212, điểm kết thúc sóng 4 đã chia toàn bộ sóng đẩy V thành hai phần theo tỷ lệ FIbonacci 0.382 và 0.618.

Nguồn: chiemtinhtaichinh

Có thể bạn quan tâm: Fibonacci Trading

(Dự đoán chính xác xu hướng thị trường với sức mạnh của Fibonacci)

ĐỌC THỬ

ĐẶT SÁCH