Kurtosis là một phép đo thống kê xác định các phần đuôi của một phân phối khác với các phần đuôi của một phân phối chuẩn. Nói cách khác, kurtosis xác định xem các phần đuôi của một phân phối nhất định có chứa các giá trị cực trị hay không.

Kurtosis là gì?

Kurtosis là một phép đo thống kê xác định các phần đuôi của một phân phối khác với các phần đuôi của một phân phối chuẩn. Nói cách khác, kurtosis xác định xem các phần đuôi của một phân phối nhất định có chứa các giá trị cực trị hay không.

Cùng với độ lệch, kurtosis là một thống kê mô tả quan trọng của phân phối dữ liệu. Tuy nhiên, hai khái niệm này không được nhầm lẫn với nhau. Về cơ bản, độ nghiêng đo lường tính đối xứng của sự phân bố, trong khi kurtosis xác định mức độ nặng của các đuôi phân phối.

Trong tài chính, kurtosis được sử dụng như một thước đo rủi ro tài chính . Một kurtosis lớn có liên quan đến rủi ro cao cho một khoản đầu tư bởi vì nó cho thấy khả năng cao của lợi nhuận cực kỳ lớn và cực kỳ nhỏ. Mặt khác, một kurtosis nhỏ báo hiệu mức độ rủi ro vừa phải vì xác suất thu được lợi nhuận cực cao là tương đối thấp.

Thừa Kurtosis là gì?

Kurtosis dư thừa là một số liệu so sánh kurtosis của một phân phối với kurtosis của một phân phối chuẩn. Kurtosis của một phân phối chuẩn bằng 3. Do đó, kurtosis dư thừa được tìm thấy bằng cách sử dụng công thức dưới đây:

Kurtosis dư thừa = Kurtosis – 3

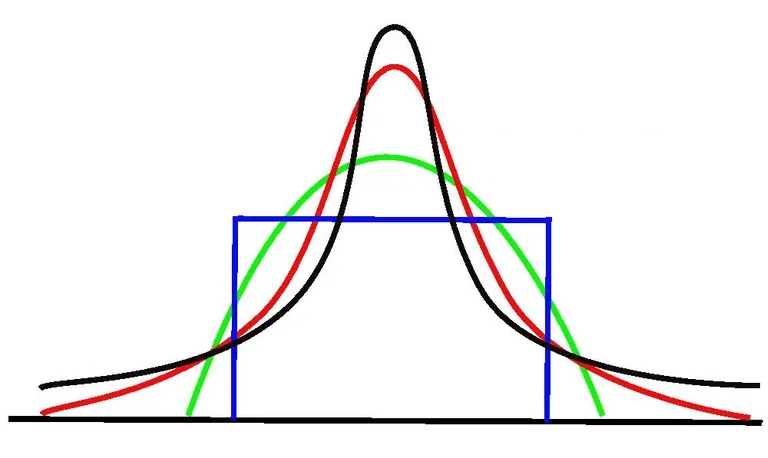
Các loại bệnh Kurtosis

Các loại kurtosis được xác định bởi kurtosis dư thừa của một phân bố cụ thể. Phần thừa kurtosis có thể nhận các giá trị dương hoặc âm, cũng như các giá trị gần bằng không.

1. Mesokurtic (có độ nhọn chuẩn)

Dữ liệu tuân theo phân phối trung bình cho thấy kurtosis dư thừa bằng 0 hoặc gần bằng không. Điều này có nghĩa là nếu dữ liệu tuân theo một phân phối chuẩn, nó tuân theo một phân phối trung bình.

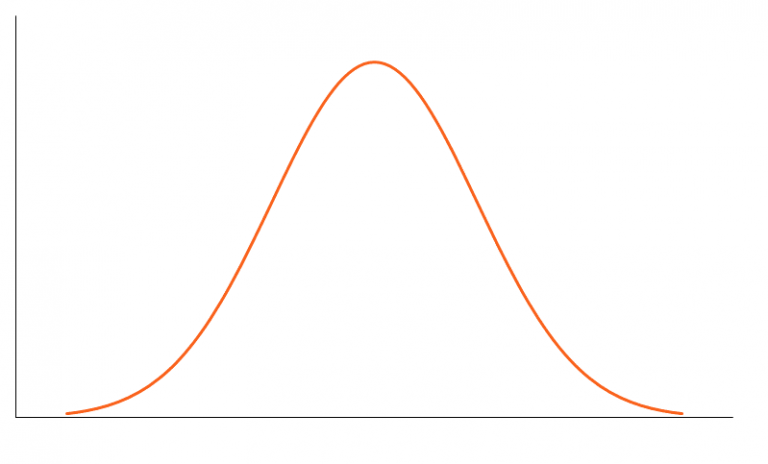
2. Leptokurtic (Phân phối leptokurtic)

Leptokurtic chỉ ra một kurtosis dư thừa dương tính. Sự phân bố leptokurtic cho thấy các đuôi nặng ở hai bên, cho thấy các giá trị chênh lệch lớn . Trong tài chính, phân phối leptokurtic cho thấy lợi nhuận đầu tư có thể nghiêng về giá trị cực đoan ở cả hai phía. Do đó, một khoản đầu tư có lợi nhuận tuân theo phân phối leptokurtic được coi là rủi ro.

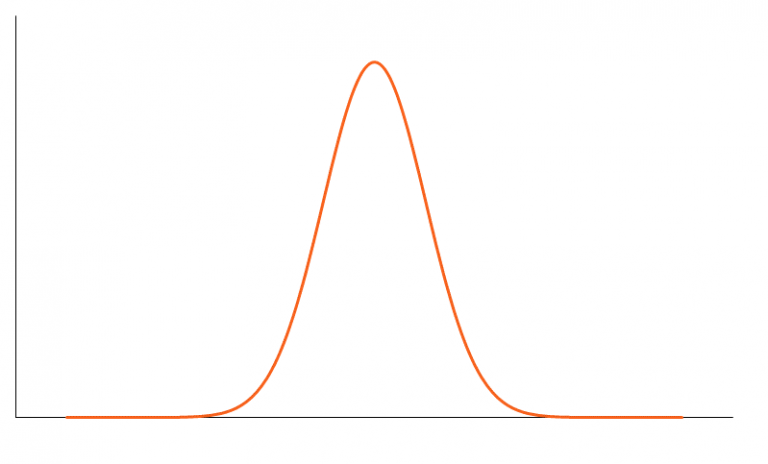
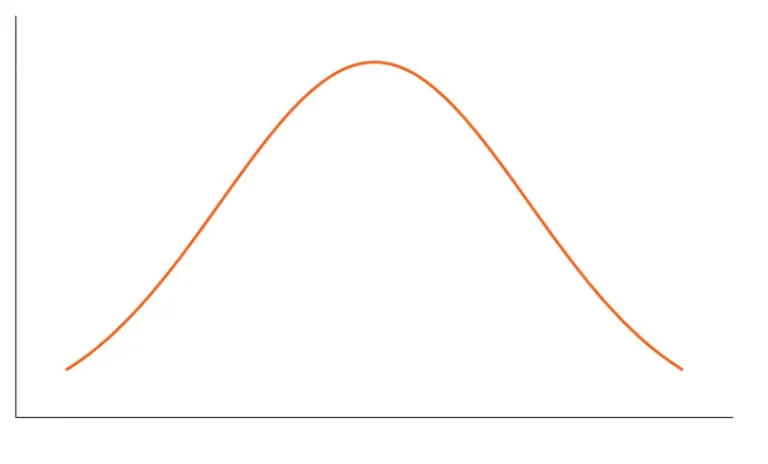
3. Platykurtic (Thú mỏ vịt)

Một phân bố của thú mỏ vịt cho thấy một kurtosis dư thừa âm tính. Các kurtosis cho thấy một sự phân bố với các đuôi phẳng. Các phần đuôi phẳng chỉ ra các giá trị ngoại lệ nhỏ trong một phân phối. Trong bối cảnh tài chính, việc phân bổ lợi nhuận đầu tư theo kiểu Platykurtic là mong muốn đối với các nhà đầu tư vì có một xác suất nhỏ là khoản đầu tư sẽ thu được lợi nhuận cực cao.

Tiến Phát

Nguồn: corporatefinanceinstitute